Keresés

"es miert specialis a 8. dimenzio ..."

Erről A Zee is ír

Interestingly, we can exploit a striking feature of SO(8), which some people
regard as the most beautiful of all groups. In particular, the two spinorial representations
8 ± have the same dimension as the vectorial representation 8 v (the equation 2 n−1 = 2n
has the unique solution n = 4). There is a transformation that cyclically rotates these three
representations 8 + , 8 − , and 8 v into each other (in the jargon, the group SO(8) admits an
outer automorphism).

"A mezőt térerőségben mérjuk, "

Hát ez nem ilyen egyszerű. Minden definiciótól függ.

"To derive Feynman diagrams, traditional texts typically adopt the

canonical formalism (which I will introduce in the next chapter) instead of the path integral
formalism used here. As we will see, in the canonical formalism fields appear as quantum
operators. "

itt pl operátor mezők vannak.

QFT könyv

Ja és Anthony Zee megmutatja azt is, hogyan számolunk kvantált gravitációs mezőt.

(Quantum Field Theory in a Nutshell )

https://en.wikipedia.org/wiki/Aharonov%E2%80%93Bohm_effect#Monopoles_and_Dirac_strings

https://en.wikipedia.org/wiki/Dual_superconductor_model

A mértékelmélet könyv gyakorlatilag a monopólusokról szól.

Amikor megérted a GT lényegét, akkor azt is megérted, miért.

(egy kis segítség: A foton mező egy "connection" a fermion fázisán.)

Happily, there is a glorious loophole in all of these arguments, first discovered by
Dirac, and magnetic monopoles play a crucial role in our understanding of the more
subtle effects in gauge theories.

Gauge Theory Cambride

http://www.damtp.cam.ac.uk/user/tong/gaugetheory/gt.pdf

Szerintem alap tankönyv a QFT-hez avagy a kvantum mező elmélethez.

Olvashatunk az őrvényekről, a monopólusokról, amivel Dirac megváltoztatta a modern fizikát, és arról, hogy miért okoz taszító erőt a spin1 vektorbozon által közvetített kölcsönhatás, és miért hoz létre vonzó erőt a spin0 spin2 mező.

Thus, a gas of vortices and antivortices appears as a gas of point “charges” with a Coulomb
interaction between them.

Quantum mechanics and magnetic monopoles

Dirac quantization of magnetic charge

Quantum Field Theory in a Nutshell 

textbook by Anthony Zee 

A foton is lehet topológiai őrvény, de ennek semmi köze a cirkuláris polarizációhoz.

https://en.wikipedia.org/wiki/Optical_vortex

Nagyon jó leírás. Gyakorlatilag mit évekig posztoltam, itt sűrítve olvasható Nigel Lockyer-től.

Higgs field was a form of superconductivity in vacuum, a relativistic quantum fluid that fills all of space.

THE HIGGS BOSON HOLY GRAIL OF PARTICLE PHYSICS Nigel Lockyer,

https://accelconf.web.cern.ch/LINAC08/papers/fr204.pdf

-Nigel Stuart Lockyer amerikai kísérleti részecskefizikus, 2013 szeptemberétől az Egyesült Államok vezető atomfizikai laboratóriumában, az illinoisi Bataviában, a Fermi National Accelerator Laboratory igazgatója.

A részecskék nem őrvények a szó hagyományos értelmében. 

Ezek topológiai őrvények, olyasmik, mint a szupravezető felszini őrvényei. (Dirac quantization of electric charge)

https://en.wikipedia.org/wiki/Quantum_vortex

https://en.wikipedia.org/wiki/Abrikosov_vortex

Olvasnivaló a témában:

forrás: Cambridge

 The surprise is that the system has angular momentum even when the particle doesn’t move.

1.4.3 Monopoles and Angular Momentum

Solid State Physics University of Cambridge Part II Mathematical Tripos

http://www.damtp.cam.ac.uk/user/tong/aqm/solidstate.pdf

Statistical Field Theory

http://www.damtp.cam.ac.uk/user/tong/sft/sft.pdf

Gauge Theory

8.2.1 Particle-Vortex Duality

http://www.damtp.cam.ac.uk/user/tong/gaugetheory/gt.pdf

Quantum Field Theory University of Cambridge Part III Mathematical Tripos

http://www.damtp.cam.ac.uk/user/tong/qft/qft.pdf

https://en.wikipedia.org/wiki/Topological_defect#Lambda_transitions

The topological solitons of that theory correspond to vortices in a superconductor; the minimum of the Mexican hat potential corresponds to the order parameter of the superconductor.

https://en.wikipedia.org/wiki/Scalar_field_theory#Gauge-field_couplings

In 2-dimensional abelian gauge theories worldsheet instantons are magnetic vortices.

https://en.wikipedia.org/wiki/Instanton#Various_numbers_of_dimensions

Nemrég vettem észre, hogy feltettek egy csomó új előadást. Most azokat nézem...

Két örvény hogyan oltja ki egymást?

https://youtu.be/IqNK7uBIVsI?t=2267

Egy elektron töltése és egy pozitron töltése...

Kell ott lenni még valaminek, mert a foton is lehetne cirkulárisan polarizált.

Nosza, dobjuk be a köztudatba egy új (még eddig fel nem fedezett) megmaradó töltés rémképét.

Hátha kapok néhány minuszt...

mi az a "triality" es miert specialis a 8. dimenzio ...

This leads to something very curious. If you are an ordinary 4-dimensional physicist you undoubtedly tend to think of spinors as "smaller" than vectors, since the spinor representations are 2-dimensional, while the vector representation is 3-dimensional. However, in general, when the dimension n of space (or spacetime) is even, the dimension of the spinor representations is 2^(n/2 - 1), while that of the vector representation is n, so after a while the spinor representation catches up with the vector representation and becomes bigger!

This is a little bit curious, or at least it may seem so at first, but what's really curious is what happens exactly when the spinor representation catches up with the vector representation. That's when 2^(n/2 - 1) = n, or n = 8. The group Spin(8) has three 8-dimensional irreducible representations: the vector, left-handed spinor, and right-handed spinor representation. 

http://math.ucr.edu/home/baez/week61.html

This automorphism group permutes the three 8-dimensional irreducible representations of Spin(8); these being the vector representation and two chiral spin representations.

https://en.wikipedia.org/wiki/Triality

This is because there are 240 lattice vectors of minimum nonzero norm (the roots of the E₈ lattice). It was shown in 1979 that this is the maximum possible number in 8 dimensions.^[10][11]

https://en.wikipedia.org/wiki/E8_lattice#Sphere_packings_and_kissing_numbers

_{<!doctype html>
<html>
<body>
<canvas width="1000" height="600" id="my_Canvas"></canvas>}

<script>

/*============= Creating a canvas ======================*/
var iradian = Math.PI / 180.0;

var canvas = document.getElementById('my_Canvas');
//gl = canvas.getContext('experimental-webgl');
var ctx = canvas.getContext("2d");
ctx.imageSmoothingEnabled = false;
ctx.translate(0.5, 0.5);
var wx = canvas.width, wy = canvas.height;

var demomode = 1;
var operatemode=0;
var zoom=320.0;
var spaceview=0;

// ##############################
// vector class
// ##############################

function vec3(vx, vy, vz) {
this.x = vx || 0;
this.y = vy || 0;
this.z = vz || 0;
};
vec3.copy = function (v1) {
var e = new vec3;
e.x = v1.x;
e.y = v1.y;
e.z = v1.z;
return e;
};
vec3.add = function(a,b) {
if (b instanceof vec3) {return new vec3(a.x+b.x,a.y+b.y,a.z+b.z );}// parm vec3
else {return new vec3(a.x+b ,a.y+b ,a.z+b );}// parm scalar
return b;
};
vec3.sub = function(a,b) {
if (b instanceof vec3) {return new vec3(a.x-b.x,a.y-b.y,a.z-b.z );}
else {return new vec3(a.x-b ,a.y-b ,a.z-b );}
return this;
};
vec3.mul = function(a,b) {
if (b instanceof vec3) {return new vec3(a.x*b.x,a.y*b.y,a.z*b.z );}
else {return new vec3(a.x*b ,a.y*b ,a.z*b );}
return this;
};
vec3.div = function(a,b) {
if (b instanceof vec3) {return new vec3(a.x/b.x,a.y/b.y,a.z/b.z );}
else {return new vec3(a.x/b ,a.y/b ,a.z/b );}
return this;
};
vec3.dot = function (v1, v2) { return v1.x * v2.x + v1.y * v2.y + v1.z * v2.z; };
vec3.cross = function (v1, v2) {
return new vec3(
v1.y * v2.z - v1.z * v2.y,
v1.z * v2.x - v1.x * v2.z,
v1.x * v2.y - v1.y * v2.x);
};
vec3.lengthV = function(v1) {
return Math.sqrt(vec3.dot(v1, v1));
};
vec3.normalize = function (v1) {
var len = vec3.lengthV(v1);
return new vec3(v1.x / len, v1.y / len, v1.z / len);
};

var v1 = new vec3(70, 50, 100);
var camx = new vec3(1, 0, 0);
var camy = new vec3(0, 1, 0);
var camz = new vec3(0, 0, 1);
var origo = new vec3(0, 0, 0);
var eye = new vec3(0, 0, 0);
var look = new vec3(80, 0, 00);

var e1 = new vec3(1, 0, 0);// basis vectors
var e2 = new vec3(1, 2, 0); e2 = vec3.normalize(e2);
var e3 = new vec3(0, 0, 1);

var velocity=0;
var velocity2=0;

// ##############################
// mouse handle
// ##############################

var drag = false;
var old_x, old_y;
var dX = 0, dY = 0;
var alpha1 = 277 * iradian;
var alpha2 = 20 * iradian;

var mouseDown = function (e) {
drag = true;
old_x = e.pageX, old_y = e.pageY;
e.preventDefault();
chkmenu(e.offsetX,e.offsetY);
return false;
};

var mouseUp = function (e) {
drag = false;
};

var mouseMove = function (e) {
if (!drag) {chkmenu(e.offsetX,e.offsetY);return false;}

dX = (e.offsetX - old_x) * 2 * Math.PI / canvas.width,
dY = (e.offsetY - old_y) * 2 * Math.PI / canvas.height;

if(operatemode==0)
{
alpha1 += dX;
alpha2 += dY;
}
if(operatemode==1)
{
zoom+=dY*30.0;
}
if(operatemode==2)
{
velocity -= dX*0.05;// right to +v
}
if(operatemode==3)
{
velocity2 -= dX*0.05;// right to +v
}

old_x = e.offsetX, old_y = e.offsetY;// page
e.preventDefault();

animate(0);
};
var mouseWheel = function(e) {
//NA scroll zoom+=e.deltaY*5.0;
}
var doKeyDown = function (e) {
// if (e.keyCode == 49) { demomode = 1; }// 1
// if (e.keyCode == 50) { demomode = 2; }
// if (e.keyCode == 51) { demomode = 3; }
}

canvas.addEventListener("mousedown", mouseDown, false);
canvas.addEventListener("mouseup", mouseUp, false);
canvas.addEventListener("mouseout", mouseUp, false);
canvas.addEventListener("mousemove", mouseMove, false);
canvas.addEventListener("wheel", mouseWheel, false);

window.addEventListener("keypress", doKeyDown, false);

// ##############################
// lines gfx
// ##############################

function qprint(xc, yc, str, color) {
ctx.font = "15px Comic Sans MS";
ctx.fillStyle = color;// '#ffff00';
ctx.textAlign = "left";
ctx.fillText(str, xc, yc);
}
function line(x1, y1, x2, y2, color)
{
ctx.beginPath();
ctx.moveTo(x1, y1);
ctx.lineTo(x2, y2);
ctx.strokeStyle=color;
ctx.stroke();
}
function transf3d(v1)
{
var sc = new vec3(0, 0, 0);
var w1 = new vec3(0, 0, 0);
w1.x = v1.x - eye.x;
w1.y = v1.y - eye.y;
w1.z = v1.z - eye.z;

sc.x = vec3.dot(w1, camx);
sc.y = vec3.dot(w1, camy);
sc.z = vec3.dot(w1, camz);

var zoom = 500;
sc.x = wx / 2 + sc.x * zoom / sc.z;
sc.y = wy / 2 - sc.y * zoom / sc.z;

return sc;
}
function line3d(v1, v2, color)
{
var sc1 = transf3d(v1);
var sc2 = transf3d(v2);

if (sc1.z > 0.0)
if (sc2.z > 0.0)
line(sc1.x, sc1.y, sc2.x, sc2.y, color);
}

var ori=0;
function arrow3d(v1, v2, color,str)
{
var sc1 = transf3d(v1);
var sc2 = transf3d(v2);
var sc3 = new vec3;
sc3.x = (sc1.x + sc2.x) / 2.0;//center
sc3.y = (sc1.y + sc2.y) / 2.0;
sc3.z = (sc1.z + sc2.z) / 2.0;

if (sc1.z > 0.0)
if (sc2.z > 0.0) {
var sc4 = new vec3;
var sc5 = new vec3;

line(sc1.x, sc1.y, sc2.x, sc2.y, color);

sc4 = vec3.copy(sc3);
sc4.x += 20.0;
if(ori==0) sc4.y -= 20.0;
else sc4.y += 20.0;
sc5 = vec3.copy(sc4);
sc5.x += 40.0;

if(str!="")
{
line(sc3.x, sc3.y, sc4.x, sc4.y, '#777777');// pointing
line(sc4.x, sc4.y, sc5.x, sc5.y, '#777777');
}

//arrow head
var xaxis=new vec3;
var yaxis=new vec3;
var zaxis=new vec3;

yaxis=vec3.sub(v2,v1);
yaxis=vec3.normalize(yaxis);
xaxis=vec3.normalize(vec3.cross(yaxis,new vec3(yaxis.z,yaxis.x,yaxis.y)));
zaxis=vec3.normalize(vec3.cross(xaxis,yaxis));

var v4=new vec3;
var k,u=12,sc=3.05;
for(var k=0;k<u;k++)
{
var aa=k*Math.PI*2.0/u;
v4=vec3.sub(v2,vec3.mul(xaxis,Math.cos(aa)*sc*0.3));
v4=vec3.sub(v4,vec3.mul(zaxis,Math.sin(aa)*sc*0.3));
v4=vec3.sub(v4,vec3.mul(yaxis,sc));

line3d(v2,v4,color);
}

// text
sc4.y -= 5.0;
if(str!="")
qprint(sc4.x, sc4.y,str,color);
}
ori=0;
}
function circle3d(p1,p2,color)
{
var r=20.0;
var p4=p1;

for(var i=0;i<41;i+=1)
{
var p3=vec3.sub(p2,p1);
p3=vec3.mul(p3,i/40.0);
var p6=vec3.add(p1,p3);// p3=p1+(p2-p1)*i/40

var ok=0;
if(p6.z>0.0)
if(p6.z<50.0) ok=1;

var aa=i*Math.PI*2.0/40.0;
p6.y=Math.cos(aa)*r-30.0;
p6.z=Math.sin(aa)*r;
if(ok==1)
if(i!=0) line3d(p6,p4,color);
p4=p6;
}
}
function circle3dold(p1,p2,color)
{
var r=20.0;
var p4=p1;

for(var i=0;i<40;i+=1)
{
var p3=vec3.sub(p2,p1);
p3=vec3.mul(p3,i/40.0);
p3=vec3.add(p1,p3);

var p33=p3;
var aa=i*Math.PI*2.0/40.0;
p33.y=Math.cos(aa)*r-30.0;
p33.z=Math.sin(aa)*r;
if(p3.z>-50.0)
if(p3.z<50.0)
if(i!=0) line3d(p33,p4,color);
p4=p33;
}
}

function sphere(alf1, alf2, ra)
{
return new vec3(
ra * Math.cos(alf1) * Math.cos(alf2),
ra * Math.sin(alf1) * Math.cos(alf2),
ra * Math.sin(alf2));
}

// ##############################
// menu
// ##############################

var menus=["lightclock","lightcones","space view","transf U(1)","Reciprocity","rot camera","zoom","velocity","vel 3rd RF"];
var xm,ym,nn,nm;
var xh=100,yh=18;
var itemsx=[];
var itemsy=[];
var itemsena=[];

function itermenu(value)
{
ctx.fillStyle = '#555555';
ctx.fillRect(xm, ym, xh, yh);

var col1='#ffffff';
var col2='#777777';
if(itemsena[nn]==1) {var q=col1;col1=col2;col2=q;}
line(xm,ym,xm+xh,ym,col1);
line(xm,ym,xm,ym+yh,col1);
line(xm,ym+yh,xm+xh,ym+yh,col2);
line(xm+xh,ym,xm+xh,ym+yh,col2);

qprint(xm+5,ym+14,value,'#ffffff');

itemsx[nn]=xm;
itemsy[nn]=ym;

ym+=27;
nn+=1;
}

function updatemenu()
{
xm=30;ym=100;nn=0;
menus.forEach(itermenu);
nm=nn;
}
function chkmenu(x,y)
{
var i,j;
for(i=0;i<nm;i++)
{
// itemsena[i]=0;

if(x>=itemsx[i])
if(x<=itemsx[i]+xh)
if(y>=itemsy[i])
if(y<=itemsy[i]+yh)
{
var ll=5;//separator
if(i<ll) for(j=0;j<ll;j++) itemsena[j]=0;//clear radio button style
else for(j=ll;j<nm;j++) itemsena[j]=0;
itemsena[i]=1;

if(i<ll) demomode=i+1;
else operatemode=i-ll;

animate(0);
}
}
}

// ##############################
// special relativity
// ##############################

var c=1,v1=0; // natural unit

function lorentz_transformation(p1,v)
{
var gamma=1.0/Math.sqrt(1.0-v*v/(c*c));

var p2=new vec3(0,0,0);
p2.x=(p1.x - v*p1.z)*gamma;
p2.y=p1.y;
p2.z=(p1.z - v*p1.x/(c*c))*gamma;// z==time component
return p2;
}
function arrowLT(p1,p2,color,ss)
{
var p1b=lorentz_transformation(p1,v1);
var p2b=lorentz_transformation(p2,v1);

if(spaceview==1) {p1b.z=0;p2b.z=0;}

arrow3d(p1b,p2b,color,ss);
}
function arrowU1(p1,p2,color,ss)
{
var p1b=lorentz_transformation(p1,v1);
var p2b=lorentz_transformation(p2,v1);

if(spaceview==1) {p1b.z=0;p2b.z=0;}

circle3d(p1b,p2b,color);
}
function qprint3d(p1,str,color)
{
var sc1 = transf3d(p1);
qprint(sc1.x, sc1.y,str,color);
}
function qprintLT(p1,str,color)
{
var p1b=lorentz_transformation(p1,v1);
// if(str!="")
qprint3d(p1b,str,color);
}

// ##############################
// main function
// ##############################

function drawscene()
{
// camera setup
camz.x = look.x - eye.x;
camz.y = look.y - eye.y;
camz.z = look.z - eye.z;
camz = vec3.normalize(camz);
camy = new vec3(0, 0, 1);
camx = vec3.cross(camz, camy);
camx = vec3.normalize(camx);
camy = vec3.cross(camx, camz);
camy = vec3.normalize(camy);

// background
var h=10;
for (var y = -300; y < 300; y += h)
for (var x = -300; x < 300; x += h)
{
line3d(new vec3(x, y,0), new vec3(x+h, y,0), '#005500');
line3d(new vec3(x, y,0), new vec3(x, y + h,0), '#005500');
}

var gray='#555555';
var red='#ff0000';
var darkred='#880000';
var green='#00cc00';
var darkgreen='#007700';
var purple='#ff00ff';
var blue='#0000ff';
var darkpurple='#880088';
var yellow='#ffff00';
var darkyellow='#888800';

// example code
v1=velocity;

if (demomode == 2)
{
for(var i=0;i<20;i++)
{
var aa=i*Math.PI*2/20.0;
var r=100.0;
var c1=r*Math.cos(aa);
var s1=r*Math.sin(aa);
arrowLT(new vec3(0,0,0),new vec3(s1,c1,100),darkred,"");

arrowLT(new vec3(s1,c1,100),new vec3(0,0,200),darkred,"");
arrowLT(new vec3(0,0,200),new vec3(s1,c1,300),darkred,"");
}

qprint(30, 45, "light cones", '#ffffff');
}

if (demomode == 1 ||demomode == 2)
{
arrowLT(new vec3(0,0,0),new vec3(0,0,300),green,"mirror1");
arrowLT(new vec3(100,0,0),new vec3(100,0,300),green,"mirror2");
arrowLT(new vec3(0,0,0),new vec3(100,0,100),red,"light");
arrowLT(new vec3(100,0,100),new vec3(0,0,200),red,"light");
arrowLT(new vec3(0,0,200),new vec3(100,0,300),red,"light");

arrowLT(new vec3(0,100,0),new vec3(0,100,300),green,"mirror3");
arrowLT(new vec3(0,0,0),new vec3(0,100,100),red,"light");
arrowLT(new vec3(0,100,100),new vec3(0,0,200),red,"light");
arrowLT(new vec3(0,0,200),new vec3(0,100,300),red,"light");

if (demomode == 1)
qprint(30, 45, "light clock", '#ffffff');
}
if (demomode == 3)
{
arrowLT(new vec3(0,0,0),new vec3(0,0,300),darkgreen,"mirror1");
/* arrowLT(new vec3(100,0,0),new vec3(100,0,300),green,"mirror2");
arrowLT(new vec3(0,0,0),new vec3(100,0,100),red,"light");
arrowLT(new vec3(100,0,100),new vec3(0,0,200),red,"light");
arrowLT(new vec3(0,0,200),new vec3(100,0,300),red,"light");*/

arrowLT(new vec3(0,100,0),new vec3(0,100,300),darkgreen,"mirror3");
arrowLT(new vec3(0,0,0),new vec3(0,100,100),darkred,"light");
arrowLT(new vec3(0,100,100),new vec3(0,0,200),darkred,"light");
arrowLT(new vec3(0,0,200),new vec3(0,100,300),darkred,"light");

spaceview=1;
arrowLT(new vec3(0,0,0),new vec3(0,0,300),green,"mirror1");
arrowLT(new vec3(0,100,0),new vec3(0,100,300),green,"mirror3");
arrowLT(new vec3(0,0,0),new vec3(0,100,100),red,"light");
arrowLT(new vec3(0,100,100),new vec3(0,0,200),red,"light");
arrowLT(new vec3(0,0,200),new vec3(0,100,300),red,"light");
spaceview=0;

qprint(30, 45, "space view of light clock (orthogonal component )", '#ffffff');
}

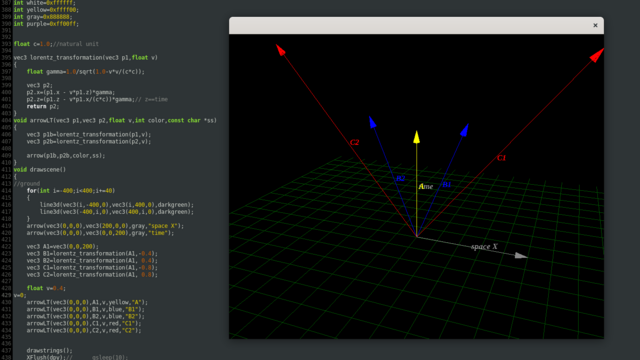
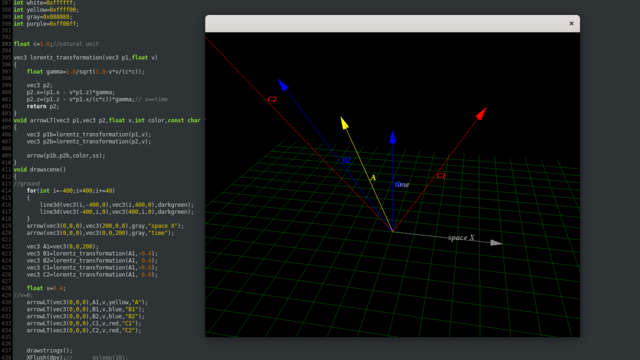
if (demomode == 4)
{
v1=velocity;

for(var m=0;m<2;m++)
for(var i=-3;i<4;i++)
for(var j=0;j<3;j++)
for(var k=0;k<2;k++)
{
var v2=0.0;
if(k) v2=velocity;

var a1=lorentz_transformation(new vec3(0+j*120,0,0+i*50),v2);
var a2=lorentz_transformation(new vec3(25+j*120,0,25+i*50),v2);
var a3=lorentz_transformation(new vec3(0+j*120,0,50+i*50),v2);

v1=-velocity2;// 3rd frame of reference
arrowLT(a1,a2,red,"");
arrowLT(a2,a3,red,"");

var color=darkyellow;
if(k==0) color=darkpurple;
var b1=lorentz_transformation(new vec3(0+j*120,0,0+i*50),v2);
var b2=lorentz_transformation(new vec3(0+j*120,0,50+i*50),v2);
arrowLT(b1,b2,color,"");

color=yellow;
if(k==0) color=purple;
b1=lorentz_transformation(new vec3(25+j*120,0,0+i*50),v2);
b2=lorentz_transformation(new vec3(25+j*120,0,50+i*50),v2);
if(m) arrowLT(b1,b2,color,"");
else arrowU1(b1,b2,color,"");

if(i>=0)
if(i<=2)
{
b1=lorentz_transformation(new vec3(-100+j*120,0,0+i*25),v2);
b2=lorentz_transformation(new vec3(100+j*120,0,0+i*25),v2);
if(k) arrowLT(b1,b2,blue,"");
else arrowLT(b1,b2,0x00ffff,"");
}
}
}
if (demomode == 5)
{
v1=velocity;

for(var m=0;m<2;m++)
for(var i=-3;i<4;i++)
for(var j=0;j<3;j++)
for(var k=0;k<2;k++)
{
var v2=0.0;
if(k) v2=velocity;

var a1=lorentz_transformation(new vec3(0+j*120,0,0+i*50),v2);
var a2=lorentz_transformation(new vec3(25+j*120,0,25+i*50),v2);
var a3=lorentz_transformation(new vec3(0+j*120,0,50+i*50),v2);

v1=-velocity2;// 3rd frame of reference
arrowLT(a1,a2,red,"");
arrowLT(a2,a3,red,"");

var color=darkyellow;
if(k==0) color=darkpurple;
var b1=lorentz_transformation(new vec3(0+j*120,0,0+i*50),v2);
var b2=lorentz_transformation(new vec3(0+j*120,0,50+i*50),v2);
arrowLT(b1,b2,color,"");

color=yellow;
if(k==0) color=purple;
b1=lorentz_transformation(new vec3(25+j*120,0,0+i*50),v2);
b2=lorentz_transformation(new vec3(25+j*120,0,50+i*50),v2);
arrowLT(b1,b2,color,"");

qprintLT(b2,i,color);//

if(((i+3)%2)==1)
{
b1=lorentz_transformation(new vec3(-100+j*120,0,0+i*25),v2);
b2=lorentz_transformation(new vec3(100+j*120,0,0+i*25),v2);
if(k) arrowLT(b1,b2,blue,"");
else arrowLT(b1,b2,0x00ffff,"");
}
}
}

v1=velocity;
arrow3d(new vec3(0,0,0),new vec3(200,0,0),gray,"space X");
arrow3d(new vec3(0,0,0),new vec3(0,0,200),gray,"time");
arrowLT(new vec3(0,0,0),new vec3(200,0,0),purple,"space X'");
arrowLT(new vec3(0,0,0),new vec3(0,0,200),purple,"time'");

// qprint(30,30,"press 1,2,3 button to select demo mode",'#888888');
qprint(30, 30, "(hold mouse button to rotate) ", '#888888');

qprint(30, 60, "velocity: "+velocity+" c", '#888888');

updatemenu();

}

var animate = function (time)
{
ctx.fillStyle = '#000000';
ctx.fillRect(0, 0, canvas.width, canvas.height); // clear bckgrn col

eye = sphere(alpha1, alpha2, zoom);//250.0
eye=vec3.add(eye,look);
drawscene();
// window.requestAnimationFrame(animate);
}

animate(0);

/*
dt=(s+dt*v)/c //forward light signal
c*dt=s+dt*v
c*dt - dt*v=s
dt*(c-v)=s
dt=s/(c-v)

dt=(s-dt*v)/c //backward light signal
c*dt=s-dt*v
c*dt + dt*v=s
dt*(c+v)=s
dt=s/(c+v)

The origin of time dilation and length contraction of specRel by lightclocks (wave interference):

t1=s/(c-v)
t2=s/(c+v)
t3=t1+t2
t2=t3-t1

t3=c/sqrt(cc-vv)
t3=1/sqrt((cc-vv)/cc)
t3=1/sqrt((1 - vv/cc) time dilation by lightclock

t2=c/sqrt(cc-vv) - s/(c-v)
s/(c-v)= c/sqrt(cc-vv) - s/(c+v) /s
1/(c-v)= c/sqrt(cc-vv)/s - 1/(c+v)
1/(c-v) + 1/(c+v)= c/sqrt(cc-vv)/s
s= c/sqrt(cc-vv)/ (1/(c-v) + 1/(c+v))
s= c/sqrt(cc-vv)/ (((c+v) + (c-v))/(cc-vv)) (c-v)(c+v) = cc +cv -vc -vv = cc-vv
s= c/sqrt(cc-vv)/ ((2c)/(cc-vv))
s= (cc-vv)c / (2c sqrt(cc-vv))
s= (cc-vv) / (c sqrt(cc-vv)) x = sqrt(x)^2
s= sqrt(cc-vv) / c
s= sqrt(1-vv/cc) length contraction
*/

</script>

</body>
</html>

"Kellene létezzen egy olyan differenciálegyenlet, amely az alapvető fizikai állandókból megadja a lehetséges elemi részecskék alapvető tulajdonságait. "

hmm... nem latszik a 683 poszt?

http://forum.index.hu/Article/viewArticle?a=153986364&t=9037567

semmi reakcio? 

vagy nem megy a szamolas? 

(nem nevetek)

http://forum.index.hu/Article/viewArticle?a=149469541&t=9116521

http://forum.index.hu/Article/viewArticle?a=149469684&t=9116521

":For example, crystal defects can look like curvature and torsion in an Einstein–Cartan spacetime. "

https://en.wikipedia.org/wiki/Induced_gravity

nem goldolkozni kell a hianyos tudasbol kiindulva

hanem olvasni

xD

"Nekem viszont az a rögeszmém, hogy az örvény energiájához tömegnek is kell tartoznia..."

A rogeszmed helyes ... 

Once formed, vortices can move, stretch, twist, and interact in complex ways. A moving vortex carries with it some angular and linear momentum, energy, and mass.

https://en.wikipedia.org/wiki/Vortex

"Néhánya azt javasolták, hogy tanulmányozzam a Dirac-egyenletet.

Azzal meg az a bajom, hogy a tömeget kívülről rakják bele.

Nekem viszont az a rögeszmém, hogy az örvény energiájához tömegnek is kell tartoznia..."

A Dirac egyenlet egy modositott hullamegyenlet, ahol egy tomegtag (mass term) is szerepel. Ez valojaban egy hullam diszperziot ir le, mint mar irtam a masik topikban.,..

https://forum.index.hu/Article/showArticle?t=9174245&la=153985873

Ez annyit jelent, hogy ket mezo csatolva van egymashoz,... ugyan ugy mint a foton es az atomracs... az anyagban az EM hullamnak diszperzioja van emiatt a csatolas miatt. 

A "nyugalmi tomeg" (rest mass) ennek egy modositott formaja:

mig a foton sok anyagon kepes athatolni, egy szupravezeton erre nem kepes... az itt kapott diszperzio hasonlit legjobban a standard modell "nyugalni tomeg" definiciojahoz...

errol mar irtam a Higgs topikban meg az SG-n, de sebaj xD

szupravezeto vs foton:

Photons inside superconductors develop a nonzero effective rest mass; as a result, electromagnetic forces become short-range inside superconductors.

https://en.wikipedia.org/wiki/Photon#Experimental_checks_on_photon_mass

es a vakuum vs W Z bosons:

n the case of the weak interaction, fermions can exchange three distinct types of force carriers known as the W⁺, W⁻, and Z bosons. The mass of each of these bosons is far greater than the mass of a proton or neutron, which is consistent with the short range of the weak force. 

https://en.wikipedia.org/wiki/Weak_interaction

Erre utalt David Tong a linkelt videoban

erre utaltam ezzel:

http://forum.index.hu/Article/viewArticle?a=152081634&t=9037567

Igan, valahogy en is igy gondolom.

Foton aram nelkul nincs toltes , nincs forras .. stb

Ez a gyűrű elektron ismerősnek tűnik.

De az a baj vele, hogy a gyűrű egy képzeletben kivágott kis darabkája töltéssel rendelkezik. Nem lenne szabad.

Biztosítani kell ugyanis a töltés oszthatatlanságát. Matematikailag is!

Nekem radikálisabb elképzelésem van.

Bármekkora darabot vágjunk ki (képzeletben) az örvényből, annak nincs töltése.

Mert a töltés az örvény egészének szimmetria tulajdonsága.

a hullamcsomag sok elemi hullam osszege ...

nyilvan egy kozegben az elemi hullamok forrasa veges ...

Ha szigoruan vesszuk a QM-et es a GR-t 

akkor a Planck tavolsag a limit 

https://www.youtube.com/watch?v=L2suMPiuog4

Loop Quantum Gravity Explained

ez alatt a ter (az LQG elmeleten belul) 2 dimenzios ....

Nyilvan valos kozegnel a 'racsallando' vagy az atlagos reszecskek kozotti tavolsag a limit...

De hat ugyanez a limit megtalalhato a QFT es QCD-ben is.

A vegletelen csunya dolgokat tudnak muvelni

Létezik a hullámoknak felső határfrekvenciájuk?

Vagy tényleg a végtelenig kell integrálni egy hullámcsomagot?

regebben linkeltem

https://en.wikipedia.org/wiki/Toroidal_ring_model

nem kell mindent eldobni, csak mert hibas... a KK theory is 'hibas' hiszen nem tartalmazza a SU(2) SU(3) szimmetriat.... de hat ki lehet igazitani a modellt

S1 helyett hasznalhatunk 6d komplex teret

https://en.wikipedia.org/wiki/Calabi%E2%80%93Yau_manifold

mi a problema a hurlemetettel: tul jo xD

nem latni az erdotol a fuszalat, amit keresunk

https://www.scientificamerican.com/article/found-a-quadrillion-ways-for-string-theory-to-make-our-universe/

Comparing path A with path B gives the non-integrable phase shift ∆ θ. Because of this phase shift, the wave front of a plane wave is pulled and the plane wave changes directions.

Unifying Geometrical Representations of Gauge Theory Scott Alsid · Mario Serna

https://arxiv.org/pdf/1308.1092.pdf

Azt hiszem a mertek-elmeletrol mar osztottam itt az eszt. Felmerulhet a kerdes: a Compton szoras egyertelmuen 'reszecske' utkozesrol szol. Ellenben a kvantum fizika minden reszlete hullamokra utal (mint peldaul :heisenberg uncertainty principle == hullam csomag fizika This trade-off between spread in position and spread in momentum is a characteristic feature of the Heisenberg uncertainty principle, and will be illustrated below.

https://en.wikipedia.org/wiki/Wave_packet)

Hogy is van ez?

Nos ha belegondolunk, minden hullam jelenseg visszavezetheto reszecskek utkozesere ... hiszen maga a folyadek vagy a levego is reszecskebol all es ezek ritmusos utkozese a hullam.

Szoval igazabol itt egyetlen 'furcsa' dolog van: a vakuum nem az aminek latszik ... nem egy ures semmi, hanem egy lathatatlan dolgokkal telezsufolt entitas ...

Feynman könyvében egy egész fejezet foglalkozik a pontszerű töltés problémájával.

De ha azt feltételezzük, hogy a töltés a "hullámfüggvény" örvényléséből származik, akkor nincs vele probléma.

A hullámfüggvény kiterjedéssel rendelkezik, a töltés pedig nem rendelhető hozzá egyetlen ponthoz, hanem a hullámfüggvény egésze viseli ezt a tulajdonságot. Messziről nézve pontszerűnek tűnhet.

Néhánya azt javasolták, hogy tanulmányozzam a Dirac-egyenletet.

Azzal meg az a bajom, hogy a tömeget kívülről rakják bele.

Nekem viszont az a rögeszmém, hogy az örvény energiájához tömegnek is kell tartoznia...

Kellene létezzen egy olyan differenciálegyenlet, amely az alapvető fizikai állandókból megadja a lehetséges elemi részecskék alapvető tulajdonságait. Egyszerűen megoldod a feltételezett differenciálegyenletet, és sorra kipotyognak belőle a létező (és esetleg még felfedezésre váró) elemi részecskék, mint kvantált megoldások.

*eliras:

  -> Yw=0

hogy a jobb kezes neutrino valojaban a supercharge

https://en.wikipedia.org/wiki/Supercharge

azt nagyon egyszeru belatni... 

a jobbkezes neutrino neutral, semleges toltesu, 

https://en.wikipedia.org/wiki/Weak_hypercharge

mivel jobb kezes -> T3=0 

mivel Q= T3 + 1/2Yw  and Q=0        -> Tw=0

spin feles, szoval

right handed neutrino == supercharge of SUSY