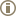QUANTUM ERASER - A MEGVALÓSULT SCHRÖDINGER-MACSKA?
Vágjunk bele a közepébe. Egy kísérlet vázát írom le, ami a híres
kettős-rés kísérlet módosítása,
EPR-párokkal és késleltetett választással. Akinek ez elsőre bonyolultan hangzik, ne ijedjen meg; a lényeget matek nélkül is fel lehet fogni és azt hiszem, megéri – nagyon meglepő dologról van szó. Úgy kezdem az ismertetést, hogy felteszem a kettős-rés kísérlet lényegének valamint az EPR-korreláció mibenlétének ismeretét.
Ha valakinek nincs ideje vagy kedve módszeresen végigolvasni, az
ugorjon a kettővel ezutáni hozzászólásra, amiben tőmondatokban összefoglaltam a tanulságokat. (Ha aztán onnan nem tér vissza a kísérlethez, akkor nem is érdekli a fizika….)
A link egy cikkre mutat, ami a kísérlet leírását és magyarázatokat tartalmaz. Quantum eraser kísérlet késleltetett választással.
Úgy indulunk, mint egy szokásos kettős-rés kísérletben. Megfelelő forrásból keltett fotonok átmennek egy falon, amin a két rés van. Ezután a módosítás: a két rés mögött nem akadálytalanul mennek tovább, hanem elhelyezünk egy
speciális kristályt, amibe beleütköznek. A kristály olyan, hogy a beleütközö fotonok egy újabb
fotonpárt keltenek benne – méghozzá EPR-korrelációval összecsatolt fotonokat. (Ism: ezek olyanok, hogy közös állapotfügvény írja le őket a szétrepülésük után is; ha a már egymástól távollévő fotonpár egyik tagján megmérjük az alapvető fizikai mennyiségeket (hely, impulzus, polarizáció stb.), akkor
egyidejűleg a másikról is megszerezzük a megfelelő információt lsd. bővebben az EPR ill. Bell-típusú kísérletekkel foglalkozó szakirodalmat).
Tehát az eredeti fotonok már megszűntek, viszont mindegyik keltett egy szétrepülő EPR-párt. Mondjuk, minden pár egyik tagja északkelet felé halad tovább (hívjuk ezeket signal-fotonoknak), a másik pedig délkelet felé (a továbbiakban idler-fotonok).
A signal-fotonokkal az történik a továbbiakban, mint a szokásos kétréses-kísérletben: haladnak egy ernyő (detektor) felé, amelyen való becsapódásuk kirajzolja a hely szerinti eloszlást. Rajtuk már nem végzünk további mérést a becsapódásig, nem kerülnek kölcsönhatásba semmivel. Nincs az útjukban olyan berendezés, ami meg tudná állapítani, hogy melyik rés közelében keletkeztek. Az ábrákon ezeket a felfelé haladó vonalak jelzik.



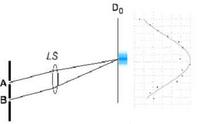
Ha tudhatjuk, melyik résen mentek át az eredeti fotonok,és így a kristály A vagy B régiójában keletkeztek az EPR-párok, akkor nincs interferencia (szemléltetés a 2. eset), ha nem tudhatjuk, akkor van (az 1.eset).
A kérdés, amire a kísérlet kifut: milyen eloszlást rajzolnak ki ezek a fotonok, illetve az egyes részhalmazaik? A válasz nemsokára, de előbb nézzük, mi történik a társaikkal.
Az idler-fotonokkal (a lefelé haladó vonalak jelzik) csinálunk lényeges dolgokat. Ők belehaladnak egy mérőberendezésbe, amiben kétféle dolog történhet velük: vagy megmérjük, melyik rés mögött keletkeztek, vagy úgy interferáltatjuk önmagukkal, hogy az ilyen helymérés a továbbiakban már nem lesz lehetséges. Tehát tkp. ezekkel a fotonokkal történik az, ami a normális kétrésesnél szokott:
vagy megszerezzük róluk a „melyik út” információt, vagy nem, (hanem hagyjuk elveszni ezt az infót, ezért eraser), hagyjuk, hogy interferáljanak.
Lényeges: ha egy idler fotonról megállapítjuk, melyik rés mögött keletkezett, akkor ez további két információt is jelent: 1. megtudjuk azt is, hogy az a foton, ami keltette őket, melyik résen ment át 2. az ő EPR-társfotonjáról is megtudjuk, melyik rés mögött keletkezett. Tehát az idlereken végrehajtott „melyik út” mérés egyben az elsődleges fotonok „melyik út” mérése is, és a signal-fotonoké is. Ill, ha nem végzünk melyik-út mérést, akkor az interferencia meghagyása is mindháromra. Ez az ábra az idlerek útjának vázlata:
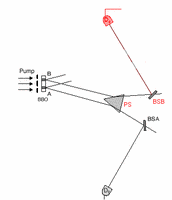
Vissza a kísérlet menetéhez: a signal-fotonok már csak elérik a detektort, de az idler-fotonok belekerülnek a számukra előkészített mérőberendezésbe. Itt 50-50%-os valószínűséggel vagy megmérik rajtuk, honnan jöttek, vagy nem. (
Fontos: ebben a kísérletben ez nem a kísérletezők döntése szerint történik, hanem véletlenül, egy nyalábosztóval, ami fele-fele valószínűséggel irányítja a fotonokat a kétféle méréshez. DE a cikkben is megemlítik, hogy más hasonló kísérletekben viszont a mérést végzők dönthetik el, mi történjen. A tanulságokon ez nem változtat, de a ténylegesen választást tartalmazó kísérletek még élesebben mutatják őket. És talán a következményeik is mások lehetnek.)
A harmadik lépés az, hogy
összefésülik a megszerzett információkat, vagyis a signal-fotonokról készített eloszlást és az idler-társaikról felvett mérési eredményeket. Ezt végzi el a CC egység (Coincidence Circuit). Vagyis ide érkezik be egyrészt a felső detektorok által regisztrált eloszlásról való információ, másrészt a társaikról való információk, és itt összepárosítják őket az EPR-párok szerint. (Gondolom; de ez nem teljesen világos, vagyis az, hogy is működik ez a CC – bár részletkérdésnek tűnik). Tehát az egész berendezés vázlata:
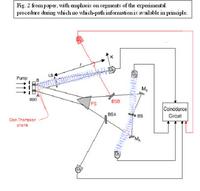
Na most térjünk vissza a
fő kérdésre: milyen eloszlást rajzolnak ki a signal-fotonok? Attól függ, mi történik a társaikkal. Akiknek a párjain nem végeznek melyik-út mérést, azok interferenciaképet alkotnak, akiknek a párjain igen, azok a másik fajta eloszlást. Ennek így is kell lennie a kvantummechanika szerint. De most annak ellenére viselkednek ilyen kétféle módon, hogy velük magukkal bármilyen mérés, kölcsönhatás történt volna. (Fontos: amennyiben más kísérletekben tényleg a mérést végzők döntenek, akkor nem látom akadályát annak, hogy egy-egy esetben a teljes mezőnyt csak melyik-út mérésnek vessék alá, vagy nem. Ekkor a teljes kép változik így; a most tárgyalt kísérletben fele-fele arányban össze van keveredve a kétféle eloszlás, és a részhalmazok változnak a másik mérés függvényében.)
Most jöhet az összefoglalás:
1.Tanulság: az interferencia szétrombolása nem annak a következménye, hogy a megfigyeléshez meg kell zavarnunk az objektumot, nem a mérési beavatkozás következménye. Nem a határozatlansági reláció miatt történik.
Pedig vagy 70 éven keresztül az volt az elgondolás, hogy azért történik. Ahhoz, hogy megfigyeljük, melyik úton halad, kölcsönhatásba kell a hoznunk valamivel, ami impulzuscserével jár; minél pontosabban mérünk, annál nagyobbal, és így a határozatlansági reláció kormányozta módon ez éppen elmossa az eredeti interferenciát. Ez volt a „common wisdom” a kérdést illetően; hosszú történet, már az Einstein-Bohr vitákban is felmerültek hasonló gondolatkísérletek, majd gondos kísérletekkel ki is mérték ezt az elmosódást. Még Feynmann is így tárgyalja a problémát. Megnyugtató is ez a kép: bár rejtélyes a viselkedés, de azért legalább látjuk a mechanizmust mögötte.
Ez az elgondolás itt megdől. Anélkül változik az interferencia a signal fotonok esetében, hogy bármilyen kölcsönhatásba kerülnének az útjuk során. Mi marad? Már Feynmann is úgy szűrte le a lényeget, hogy: ha az elrendezés olyan, hogy nincs mód annak magállapítására, melyik résen mennek át, akkor interfeernciakép lesz; ha meg van mód a melyik-út információ megszerzésére,akkor nem lesz interferencia. Ez most is igaz.
Természetesen nem állíthatjuk, hogy azok a kísérletek és a határozatlanságra alapuló gondolatmenet rosszak lettek volna. Teljesen jók, ellenőrzöttek. Azok is okozzák az interfencia elmosását, de kiderült, hogy nem általános érvényűek, nem ők a lényegesek az egészben.
Quantum eraser delayed choice
de a majom még csak most fog fürdeni igazán!